線形回帰、カーネル線形回帰をRで実装する
http://d.hatena.ne.jp/sesejun/20090401/p1 で紹介したカーネル多変量解析本の続き。
演習があるべきだ、と言ったが一般にカーネル法だと、与えられた点の数だけ次元を持つ正方行列を扱うので、演習を作っても手で解くのがつらい。だから、こんな風にソースコードを入れてみるのは、どうかと思ったので、このエントリを書いてみた。
線形回帰からカーネル線形回帰までをRで書いてみる(行列扱うのが楽なので)。式番号は、カーネル多変量解析の本に出てくる式番号である(まだ式番号をつけていないところが多いので、後日つけます付けました。2009/4/3)。
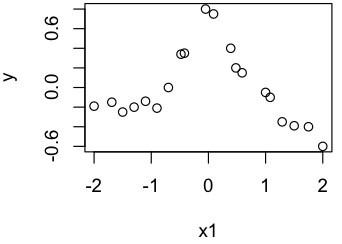
- まずは単なるXYプロット。正規分布を鋭角にした感じの点20個。図1.3(P9)の点を真似た。
x1 <- c(-2,-1.69,-1.5,-1.3,-1.1,-0.9,-0.7,-0.48,-0.42,-0.05,0.09,0.39,0.48,0.59,1.0,1.08,1.29,1.5,1.75,2.0) y <- c(-0.19,-0.15,-0.25,-0.2,-0.14,-0.21,0,0.34,0.35,0.8,0.75,0.4,0.2,0.15,-0.05,-0.1,-0.35,-0.39,-0.4,-0.6) plot(x1,y)
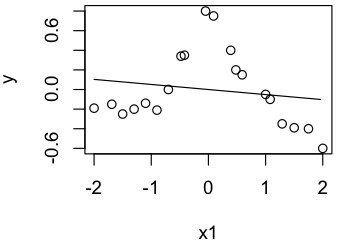
- 線形回帰
ここでは、原点を通る直線での回帰を考える。与えられた点の二乗誤差を最小にする直線が、y' = w・X'と書けるとすると、w = (X^t X)^-1 X^t Y (式1.7, P6)なので、次のように回帰直線が書ける。
w <- solve(t(x1) %*% x1) %*% t(x1) %*% y tangent <- function(x) w[1] * x curve(tangent, add = TRUE)
まず、20点x20点のグラム行列を計算する。ここではカーネルとしてガウスカーネルを利用する。
# データの個数。x1とyの大きさは同じと思っている。
n <- length(x1)
# カーネル関数を用意する。ここの関数を変更すれば、他のカーネルが利用できる。
# P6, 式1.8参照。
slope <- 0.5
kf.gauss <- function(x1,x2) exp(-1.0 * slope * (x1-x2)^2)
# グラム行列の初期化。全部1.0で埋める。
gram <- matrix(data=1.0,nrow=n,ncol=n)
# グラム行列を計算する
gram <- sapply(x1, function(x) kf.gauss(x,x1))
# 各行毎に計算した場合、こう書ける。for(i in 1:n) { gram[i,] <- sapply(x1, function(x) kf.gauss(x,x1[i])) }この後、Y = \sum_i \alpha_i \times k(x1_i,X) の \alphaを求めるのだが、計算したグラム行列のランクが14しかないため、逆行列が求められず
# 重みalphaを求める(P8, 式1.14) alpha <- solve(gram) %*% y
とすると、この例題ではエラーになる*1。ここでは少しさぼって、20点中14点だけを使って計算する。
# ランク落ちしないように、14点選ぶ pivot <- qr(gram)$pivot[1:14] # pivotを表示すると次のように前半の点が多く選択されている # [1] 1 2 3 4 5 6 7 8 9 10 12 14 16 19 # 選んだpivotを使って、alphaを計算する alpha <- solve(gram[pivot,pivot]) %*% y[pivot]
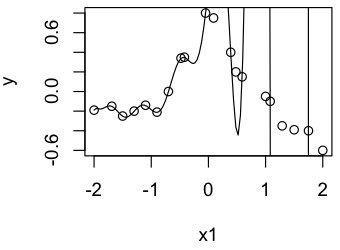
この求めたalphaを使って線を書いてみよう。
plot(x1, y) # 曲線を描くための式を作る approxcurve <- function(x) sapply(x, function(y) kf.gauss(x1[pivot], y) %*% alpha) # 曲線を描く curve(approxcurve, add=TRUE)
次のようになる。pivotに選ばれている点を通過する曲線が引かれる。pivotに選ばれていない点は値を曲線を大きく外れる。pivotが前半(左の方)の点を取っているため、左半分は曲線が合うが、右が大きな振幅を持つ。
この後、L2の正則化項を入れてなめらかにする。
さて、正則化項を入れて計算し、表示してみよう。この例ではグラム行列はランク落ちしていないので、逆行列が解析的に求まる。
lambda <- 0.01 # 正則化項を入れる。P10, 式1.17 gram_L2 <- gram + diag(20)[] * lambda alpha_L2 <- solve(gram_L2) %*% y # 曲線を描くための式を作る approxcurve_L2 <- function(x) sapply(x, function(y) kf.gauss(x1, y) %*% alpha_L2) plot(x1,y) # 曲線を描く curve(approxcurve_L2, add=TRUE)
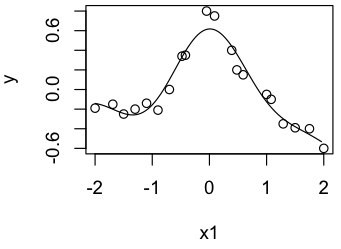
ちなみにここで、alpha_L2の中身を見ると、正の点は曲線の上に、負の点は曲線の下に来ていることがわかる。
> alpha_L2
[,1]
[1,] -4.7979759
[2,] 5.0760763
[3,] -0.6010463
[4,] 5.7777910
[5,] 6.9328202
[6,] -12.4335841
[7,] -10.0286282
[8,] 0.8929749
[9,] -4.0140095
[10,] 18.6883873
[11,] 14.0857747
[12,] -4.1295938
[13,] -16.0743362
[14,] -10.3258498
[15,] 7.5469446
[16,] 8.2134225
[17,] -5.1633123
[18,] -1.0657784
[19,] 5.9408615
[20,] -5.3157945lambdaの値を変えると正則化の割合が変わる。たとえば、lambdaを1にして、線を上書きすると次のように、正則化項が強すぎて、より平坦な曲線が描かれる
lambda <- 1 gram_L2 <- gram + diag(20)[] * lambda alpha_L2 <- solve(gram_L2) %*% y curve(approxcurve_L2, add=TRUE)
最後に、Leave one out cross varidation (LOOCV)をした時の二乗誤差を求めよう。
カーネル線形回帰では、解析的にLOOCV時の二乗誤差平均が求まる。(P36, 式2.39)
h <- solve(gram_L2) %*% gram y_tilda <- solve(gram_L2) %*% gram %*% y y_diff <- y-y_tilda sum((y_diff / (1-diag(h)))^2) / n # 1個ずつ求めて和を取るには、cv<-0で初期化の後、 # for(i in 1:20) cv <- cv + (y_diff[i]/(1-h[i,i]))^2 # cv / n # とする。